
ViniyogIndia 🚀 Momentum
Curated portfolio of strongly trending stocks
Aggressive
2Y CAGR#
35.14%
Returns*
28.56%
Benchmark*
12.75%
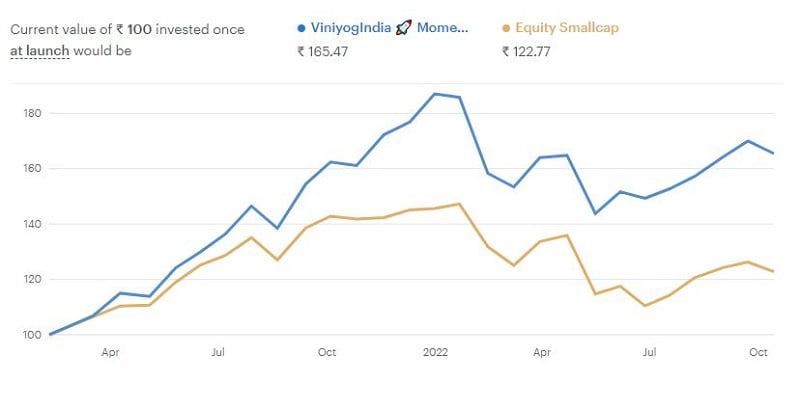
Quantitative portfolio of Stocks & ETFs. Balanced monthly. Past performance no guarantee of future results. Read full disclaimer

ViniyogIndia ☔ All Weather
Curated portfolio of Low-Risk Stocks & ETFs
Conservative
2Y CAGR#
26.03%
Returns*
26.06%
Benchmark*
13.1%
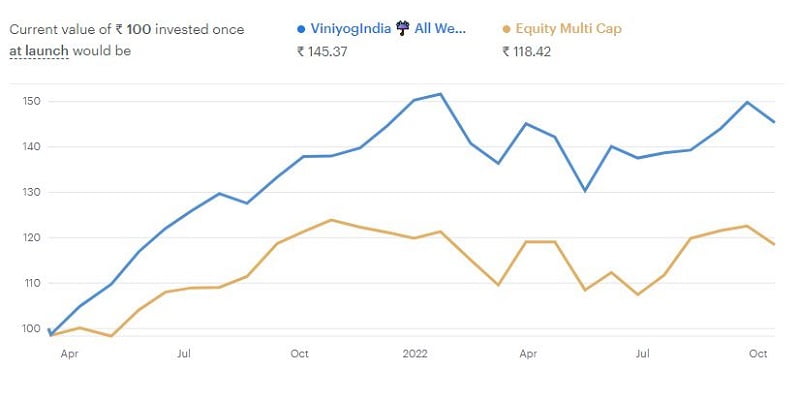
Quantitative portfolio of Stocks & ETFs. Balanced monthly. Past performance no guarantee of future results. Read full disclaimer.

ViniyogIndia ⚖ Balanced
Curated portfolio of high-quality businesses
Moderate
2Y CAGR#
33.16%
Returns*
24.83%
Benchmark*
12.1%
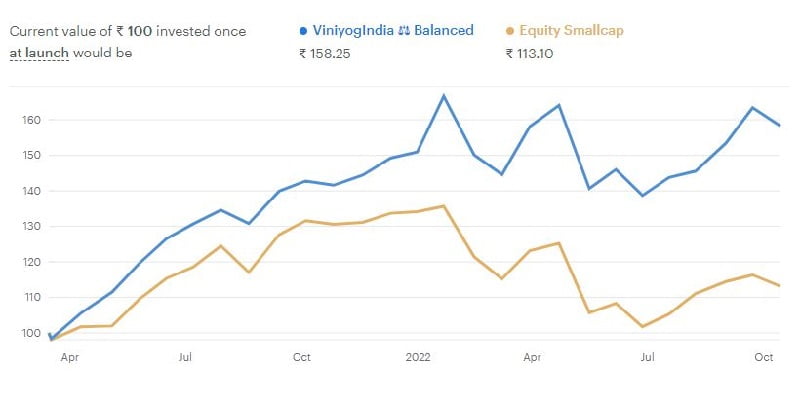
Quantitative portfolio of Stocks & ETFs. Balanced monthly. Past performance no guarantee of future results. Read full disclaimer.

ViniyogIndia 🧩 Multifactor
Multifactor portfolio of stocks with limited risk management
Moderate
2Y CAGR#
22.93%
Historical Returns *
24.28%
Benchmark
12.1%
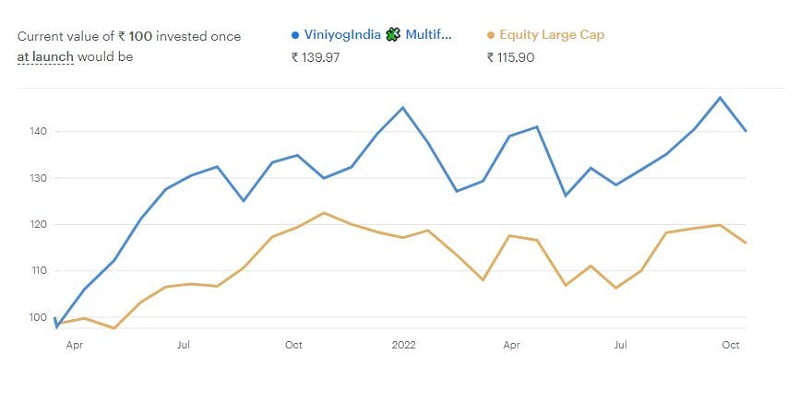
Quantitative portfolio of Stocks & ETFs. Balanced monthly. Past performance no guarantee of future results. Read full disclaimer.
* Back-tested returns. Index returns represent actual returns for the back-test period. # Actual Inception till date returns as on 15th October 2022, annualized. Graph represents actual performance of strategy (blue) & benchmark (red) since inception.
Which Portfolio is best suited for me?

Most investors make investment decisions based on historical performance. This indeed is a very wrong approach.
Investing in variable-income instruments such as stocks require ability to withstand volatility, therefore, success is largely dependent on your risk appetite.
With our newly introduced Robo Advisory service, you can now know your Risk Profile easily and decide which portfolio is best suited for you.
What is Quantitative Factor Investing
Over the years, academic community have tried to come up with various models trying to explain asset returns. These models, or asset pricing models as they are usually called, describe expected returns of financial assets, such as stocks, bonds, etc. using various characteristics or factors.
Simply put, factor can be considered as a quantitative representation of a qualitative theme that can be used to explain asset returns.
A simple example is Capital Asset Pricing Model or CAPM, which says, expected return of an asset is Risk Free Rate, plus a constant times market risk premium (expected market returns minus risk free rate)
Ri = Rf +βi(Rm – Rf)
Ri is the expected return on asset i; Rf is the risk-free rate; βi is the beta of the investment; and Rm is the expected return of the market.
Despite its popularity, CAPM is simplistic and is often criticized for its inability of explain asset returns based on empirical data. In particular, multiple studies indicated that value stocks and small cap stocks tends to outperform growth and large cap stocks respectively. This led Kenneth French and Eugene Fama to come up with a 3 Factor model that had value and size as two additional factors. Mark Carhart subsequently added a fourth factor, which was the momentum factor.
Ri – Rf =αi +βi,m(Rm – Rf) + βi,SMB(SMB) + βi,HML(HML) + βi,WML(WML) + εi
α is the intercept of the regression line; (SMB) is the return of the size factor, Small Minus Big; (HML) is the return of the value factor, High Minus Low, (WML) is the return of the momentum factor, Winner Minus Looser; ε is the residual of the regression model
Subsequently, many more factors have been identified to explain asset returns and newer factors are getting discovered by academia and industry alike. These factors can be used to develop models for systematic, rule-based trading, using software programs.