What is biggest secret to wealth creation? We’ve all heard stories of legends who started their career with nothing, yet went on to create humongous wealth through investing. What is the single biggest secret behind their success? The answer might surprise you, as it can be found wrapped inside an ancient Indian chess puzzle.
18th century French mathematician Montucla beautifully reveals this secret through what is arguably the true story of chess invention.
Wealth creation and the game of chess
According to J F Montucla (1725 – 1799), the game of chess – or Chaturanga in Sanskrit – was invented by an Indian named Sessa, son of Dahir (1, 2, 4). When Sessa presented his invention to the ruler of the country, king Shirahm (Sri Rama?), the latter was so pleased that he offered Sessa whatever he desired.
Contrary to our experience with fairy tales, Sessa didn’t ask for the princess, instead pronounced a modest wish. He requested to be rewarded with a few grains of rice* calculated in the following manner – he should be offered one grain of rice for the first square of the chess board, two grains for the second, four for the third, and so on, doubling up each time until the last or 64th square is reached.
The king laughed it off as an insignificant prize unworthy of his invention, but Sessa remained firm. So the King ordered the prime minister to fulfil Sessa’s desire who called for the treasurer. However, when the treasurer revealed result of the calculation the king was in a shock. The treasurer reported that the entire grain reserve of the kingdom was inadequate to meet Sessa’s desire!
The story goes that the king then sent for Sessa and said that he now admired him even more now for his mathematical ability than for invention of the game. Although a less romantic version tells that Sessa was beheaded for his impertinence.
* Wheat or corn according to other versions
So how many grains of rice did Sessa ask for?
Mathematicians’ today call this problem as the wheat and chessboard problem, based on the wheat version of the story (5, 6). 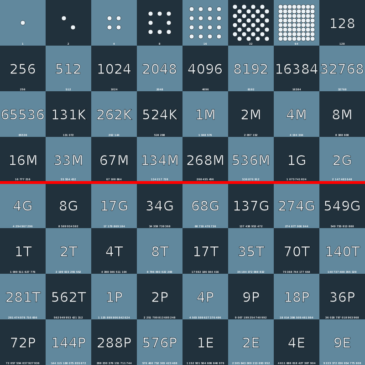
You can calculate the amount of rice or wheat requested by Sessa as follows:
20 + 21 + 22 + 23 + … + 263 = 2n – 1 = 264 – 1
= 18,446,744,073,709,551,615 grains of rice
= 461,168,602,000 MT (Ref. MP **)
= USD $300T at current market price
= About the entire wealth on the planet!
Starting with a single grain of rice, try doubling it every successive day … 2 grains on the 2nd day, 4 on the 3rd and so on… by little over 2 months (the 64th day) you will end up amassing the entire wealth of the planet! (Poor Jeff Bezos!!)
No wonder, Einstein termed compounding as the eighth wonder of the world!
Rate of return required to double wealth, or move to the next square
Below table shows the rate of return needed to double wealth or move to the next square in the chessboard. Data considers different investment and rebalancing periods, before and after tax.
At 10% LTCG, you need to compound roughly at 28% (depending on how frequently you rebalance the portfolio) to move to the next square once every 3 years.
Wealth creation secret of legendary investors
Greatest investors around the world are individuals who have been successful in compounding money at above average rates consistently over long periods of time. Take the following statistics for example (7):
- Warren Buffett: 20.8% CAGR over 50 years, 1965-2015, Berkshire Hathaway*
- Carl Icahn – 31% between 1968 & 2011 (43 years)
- Michael Steinhardt – 24.5% over 28 years, from 1967 to 1995 (after 20% cut of profits)
- Peter Lynch: 29% CAGR, between 1977 & 1990 (13 years), beating S&P500 11 out of 13 years
- Joel Greenblatt: 48% CAGR over 10 year
- Seth Klarman: ~20% CAGR over 34 years
- Benjamin Graham: ~20% CAGR over 20 years
- Jim Simons: 66.1% over 30 years, 1988 – 2018
Looking at the above data, the uninitiated might wonder why WB at 20.8% CAGR is considered arguably the greatest investor. While Berkshire Hathaway’s 50 years returns are around 20%, for the first 43 years of his career between 1950 & 1993 however, Buffett generated 31% CAGR returns similar to Carl Icahn. The compounding rate will decline with time as the size of the portfolio grows, eventually becoming indistinguishable from market returns.
Exponential growth & the legend of Paal Payasm**
We conclude this piece with another legend. The legend goes that the tradition of serving Paal Paysam to visiting pilgrims started after a game of chess between the local king and the lord Krishna himself (3). The king was very enthusiastic about chess and would frequently challenge wise visitors to a game. One day the king challenged a traveling sage to the game. To motivate his opponent the king offered any reward that the sage could name. The sage modestly asked just for a few grains of rice in the same manner that we now know as the wheat & chessboard problem.
 The king lost the game. True to his word, he ordered for a bag of rice to the chess board. Then started placing rice grains according to the arrangement: 1 grain on the first square, 2 on the second, 4 on the third, 8 on the fourth and so on.
The king lost the game. True to his word, he ordered for a bag of rice to the chess board. Then started placing rice grains according to the arrangement: 1 grain on the first square, 2 on the second, 4 on the third, 8 on the fourth and so on.
Following the exponential growth of the rice payment the king quickly realized that he was unable to fulfil his promise because on the twentieth square the king would have had to put 1,000,000 grains of rice. On the fortieth square the king would have had to put 1,000,000,000 grains of rice. And, finally on the sixty fourth square the king would have had to put more than 18,000,000,000,000,000,000 grains of rice which is allegedly sufficient to cover the whole territory of India with a meter thick layer of rice. At ten grains of rice per square inch, the above amount requires rice fields covering twice the surface area of the Earth, oceans included.
At that point lord Krishna reveals his true identity to the king and tells him that he need not pay the debt immediately but can do so over time. That is why to this day visiting pilgrims are still feasting on Paal Paysam and the king’s debt to lord Krishna is still being repaid.
*Wheat or corn according to other versions
**Paal payasam is a traditional Indian desert prepared from milk, rice, fruits, etc., often used as prasadam or offerings in temples
References
- Histoire des Mathématiques, J F Montucla.
- The Tower of Hanoi, Myths & Maths, Andreas M Hinz.
- Exponential growth & the legend of Paal Payasam
- Wikipedia – Sessa & Chaturanga
- Wikipedia – Wheat & Chessboard Problem
- Mohnish Pabrai – Columbia Compounding Presentation
- ValueWalk – Actual returns of world’s greatest investors





